预防医学/相关回归分析
| 医学电子书 >> 《预防医学》 >> 相关回归分析 |
提要 相关回归的意义,原理;小样本的直线相关和回归分析;相关系数和回归系数的意义及假设检验;应用直线相关和回归分析时的注意事项。
在医学上,许多现象之间都存在着相互联系,例如身高与体重,体温与脉搏,年龄与血压,钉螺与血吸虫感染等。而有些事物的关系是互为因果的,如上述钉螺是因,感染血吸虫是果;但有时回果不清,只是伴随关系。例如父母的兄弟,兄高,弟也可能高,但不能说兄是因、弟是果,这里不是因果关系,而可能与社会条件、家庭经济、营养、遗传等因素有关。
相关是解决客观事物或现象相互关系密切程度的问题,而回归则是用函数的形式表示出因果关系。有相关不一定因果关系;反之,有因果关系的,一定有相关。我们称“因”的变量叫![]() ,习惯上用Y表示。以横轴代表自变量X,纵轴代表依变量Y,可以将一群观察事物的两种关系在坐标图上以P(X,Y)的方法定位,作出一群点图,便可在体上看出两者的关系,例如图22-1。
,习惯上用Y表示。以横轴代表自变量X,纵轴代表依变量Y,可以将一群观察事物的两种关系在坐标图上以P(X,Y)的方法定位,作出一群点图,便可在体上看出两者的关系,例如图22-1。
图22-1(A)表示血压(依变量)随年龄(自变量)增长而增高,其图像性质与(B)一样称正相关(positive correlation);图(C)的依变量随自变量的增加而减少,称为负相关(negative correlation);若二者没有关系,则称无相关(如图D、E、F)。
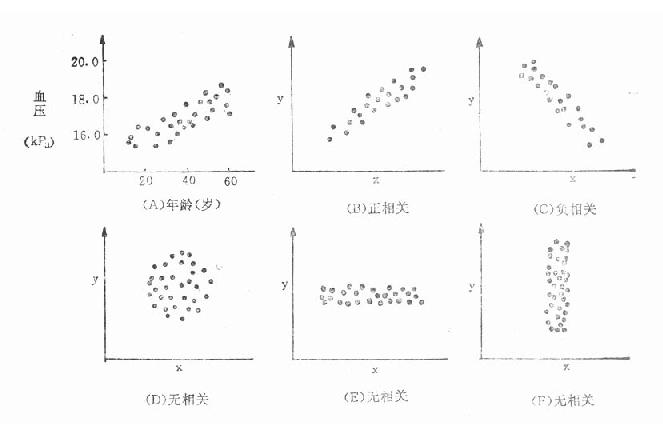
图22-1 年龄与血压相关(A)和五种有代表性点图(B~F)
根据实际资料,用数学的方法求出一条曲线(或直线),使我们能够从一个自变数推算出相关的依变量的值,这条线就叫回归线。回归线有直线和曲线两种。本章仅介绍直线相关与回归分析。
例22.1 某产科医师发现产妇尿液中雌三醇含量与初生儿体重有相关现象,因此检查了31例待产妇24小时的尿雌三醇含量,并记录下各产儿初生体重,统计如表22-1。作者意欲通过测定尿中雌三醇含量以间接预测初生儿体重,以便对低出生体重儿采取预防性措施。
表22-1 待产妇尿雌三醇含量与初生儿体重统计
| 编号(1) | 尿雌三醇mg/24h(2) | 初生儿体重kg(3) | 编号(1) | 尿雌三醇mg/24h(2) | 初生儿体重kg(3) |
| 1 | 7 | 2.5 | 17 | 17 | 3.2 |
| 2 | 9 | 2.5 | 18 | 25 | 3.2 |
| 3 | 9 | 2.5 | 19 | 27 | 3.4 |
| 4 | 12 | 2.7 | 20 | 15 | 3.4 |
| 5 | 14 | 2.7 | 21 | 15 | 3.4 |
| 6 | 16 | 2.7 | 22 | 15 | 3.5 |
| 7 | 16 | 2.4 | 23 | 16 | 3.5 |
| 8 | 14 | 3.0 | 24 | 19 | 3.4 |
| 9 | 16 | 3.0 | 25 | 18 | 3.5 |
| 10 | 16 | 3.1 | 26 | 17 | 3.6 |
| 11 | 17 | 3.0 | 27 | 18 | 3.7 |
| 12 | 19 | 3.1 | 28 | 20 | 3.8 |
| 13 | 21 | 3.0 | 29 | 22 | 4.0 |
| 14 | 24 | 2.8 | 30 | 25 | 3.9 |
| 15 | 15 | 3.2 | 31 | 24 | 4.3 |
| 16 | 16 | 3.2 |
资料来源:RosnerB:Fundamentals of Biostatistics P.346,Duxbury Press,1982
| 关于“预防医学/相关回归分析”的留言: | |
|
目前暂无留言 | |
| 添加留言 | |